이진 관계와 속성
세트의 예에 대한 광범위한 관계그 정의로 시작하여 역설에 대한 분석적 분석으로 끝나는 수많은 개념이 수반됩니다. 세트에 대한 기사에서 논의 된 다양한 개념은 무한합니다. 비록 우리가 이중 유형에 관해 말할 때, 이것은 여러 양 사이의 2 진 관계를 의미합니다. 또한 사물이나 문장들 사이.
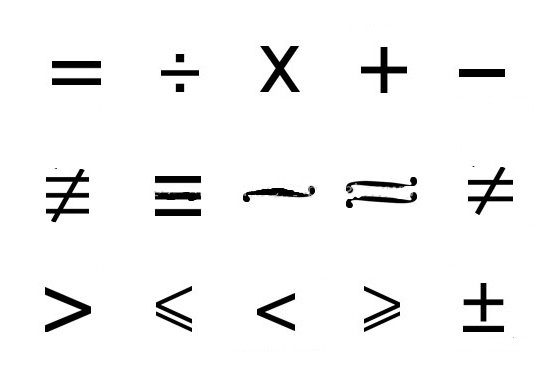
원칙적으로 이진 관계는 다음과 같이 표시됩니다.생각의 객체를 만들어, R은 개인 사이의 관계가 어떤 형태의 표시이다 - XRX는 R 필드에 X의 값을, 같은 속성이 재귀 호출하면 기호 R, 즉 x와 여기서 x,이다. 비문을 해독 마지막으로 암시의 조합과 유사한 기호, "만약 ... 그 다음 ..."그리고, (XRY UY는 Rz) - 동시에, 명시 적 또는 xRy® yRx 경우, 그것은 ® 대칭 상태에 대해 말한다. U의 기호, 전이의 관계에 대해 이야기 ®xRz -이 함께합니다.
동시에 발생하는 이진 관계반사성, 대칭성 및 이행성을 동등성의 상관 관계라고합니다. 관계 f는 함수이고, <x, y> V f와 <x, z> V f에서 등호 y = z가옵니다. 간단한 2 진 함수는 특정 순서로 위치한 두 개의 간단한 인수에 쉽게 적용될 수 있으며이 경우에만 특정 경우에 취해진이 두 표현식에 대한 값을 제공합니다.
f가 x를 y로 맵핑하고,

전술 한 내용에 기초하여, 2 진 관계의 등가 관계는 다음과 같은 속성에 의해 결정됩니다.
- 반사율 - 비율 (M ~ N);
- 대칭성 - 평등 M ~ N이면 N ~ M이 될 것입니다.
- 과도 성 (transitivity) - 두 개의 등식 M ~ N과 N ~ P이면 결과 M ~ P
이진 관계의 명시된 특성을 고려하십시오.자세한 내용. 반사성은 연구 된 세트의 각 요소가이 평등에있는 특정 관계의 특성 중 하나입니다. 예를 들어, 숫자 a = c와 a ³ c 사이에는 항상 a = a, c = c, a ³ a, c ³ c가 있으므로 반사 연결입니다. 동시에, 불평등 관계 a> c는 불평등 a> a의 존재가 불가능하기 때문에 반사적이지 않다. 이 속성의 공리는 aRc® aRa Ù cRc 기호로 인코딩됩니다. 여기서 ® 기호는 "매력적"(또는 "함축")을 의미하며 기호는 공용어 "and"(또는 연결 기호)의 역할을합니다. 이 진술로부터, aRc의 진실의 경우, aRa와 cRc의 표현 또한 참이된다.

대칭은 관계가 수반된다.사고 객체가 교체 된 경우, 즉 대칭 상호 연관성이있는 경우 객체의 재배치가 "2 진 관계"유형의 변환으로 이어지지는 않습니다. 예를 들어, 동등 관계 a = c는 관계 c = a의 등가성 때문에 대칭입니다. 또한 ¹c의 판단은 ¹a와의 연결에 응답하기 때문에 동일합니다.
전이 집합은 다음과 같은 속성입니다.여기서 다음 요구 사항이 충족됩니다. y Î x, z Î y ® z Î x, 여기서 ®는 "if ..., then ..."단어를 대체하는 기호로 나타납니다. 수식은 다음과 같이 구두로 읽습니다. "y가 x에 의존하면 z는 y에 속하며 z는 또한 x에 종속됩니다".







