정보 과학 - 번호 체계. 번호 시스템 유형

컴퓨터 과학 과정에서 학교와 관계없이또는 대학에서는 번호 체계와 같은 개념에 특별한 장소가 주어집니다. 일반적으로 몇 가지 수업 또는 실용적인 수업이 할당됩니다. 주요 목표는 주제의 기본 개념을 마스터하고 숫자 시스템의 유형을 연구 할뿐만 아니라 2 진수, 8 진수 및 16 진수 산술을 익히는 것입니다.

이것은 무엇을 의미합니까?

우리는 기본 개념의 정의부터 시작합니다. 교과서 정보학 마크로서 숫자 시스템은 숫자를 쓰는 시스템으로 특수 알파벳이나 특정 숫자 세트가 사용됩니다.

숫자의 값이 숫자의 해당 위치에서 변경되는지 여부에 따라 두 가지가 눈에 띄게 나타납니다.

위치 시스템에서 숫자 값이 변경됩니다.번호에 그녀의 위치와 함께. 따라서 숫자 234를 취하면 숫자 4는 숫자 1을 의미하지만 번호 243을 고려하면 숫자가 이미 수십이 아니라 단위를 의미합니다.

비 위치 시스템에서, 숫자의 값은 정적이며,번호의 위치와 상관없이 가장 눈에 띄는 예는로드 시스템입니다. 각 시스템은 대시로 표시됩니다. 지팡이를 부착하는 위치에 관계없이 번호의 값은 하나씩 만 변경됩니다.

비 위치 시스템

비 위치 시스템은 다음과 같습니다.

하나의 시스템으로 간주됩니다.처음. 숫자 대신 막대기가 사용되었습니다. 숫자가 클수록 숫자 값이 커집니다. 이런 식으로 기록 된 숫자의 예를 들어보세요. 영화 속에서 바다에서 길을 잃은 사람들, 죄수들, 돌이나 나무의 노치로 매일을 축하하는 사람들에 대해 이야기 할 수 있습니다.
로마 대신에 숫자가 사용되었습니다.라틴 문자. 그들을 사용하여, 당신은 어떤 숫자를 쓸 수 있습니다. 또한 그 값은 숫자로 구성된 숫자의 합과 차를 사용하여 결정되었습니다. 숫자의 왼쪽에 작은 숫자가 있으면 오른쪽 숫자에서 왼쪽 숫자를 빼고 오른쪽 숫자가 왼쪽 숫자보다 작거나 같으면 값을 합산합니다. 예를 들어, 숫자 11은 XI 및 9 - IX로 기록됩니다.
숫자가 특정 언어의 알파벳을 사용하여 표시되는 문자. 그들 중 하나는 일련의 글자가 소리 나는 것뿐만 아니라 수치를 가지고있는 슬라브 계 (Slavic system)입니다.
웨지 화살표 - 기록을 위해 두 심볼을 사용할 수 바빌로니아 시스템.
이집트에서는 숫자를 나타내는 데에도 특수 기호가 사용되었습니다. 숫자를 쓸 때 각 문자는 9 번 이상 사용할 수 없습니다.

위치 시스템

정보 과학 위치 번호 시스템에 많은 관심이 쏟아집니다. 여기에는 다음이 포함됩니다.

이진;
8 진수;
십진법;
16 진법;
시간을 계산할 때 사용되는 16 진수입니다 (예 : 분 - 60 초, 한 시간 - 60 분).

각각은 녹음, 번역 규칙 및 산술 연산을위한 자체 알파벳이 있습니다.

십진법

이 시스템은 우리에게 가장익숙한. 0부터 9까지의 숫자를 사용하여 숫자를 기록합니다. 그들은 또한 아랍인이라고 불린다. 숫자의 위치에 따라 숫자, 단위, 수십, 수백, 수천 또는 수백만을 나타낼 수 있습니다. 우리는 어디에서나 그것을 사용하며, 산술 연산이 숫자에 대해 수행되는 기본 규칙을 알고 있습니다.

이진 시스템

컴퓨터 과학의 주 번호 시스템 중 하나는 바이너리입니다. 단순성으로 인해 컴퓨터는 십진법보다 몇 배나 빠른 성가신 계산을 수행 할 수 있습니다.

숫자를 기록하려면 0과 1 두 개의 숫자 만 사용됩니다. 동시에 숫자의 0 또는 1 위치에 따라 값이 변경됩니다.

처음에는 컴퓨터가 필요한 모든 정보를받은 바이너리 코드를 사용했습니다. 이 경우, 장치는 전압에 의해 전달되는 신호의 존재를 의미하고, 0은 존재하지 않는다는 것을 의미합니다.

8 진법

또 다른 유명한 컴퓨터 시스템0에서 7까지의 숫자가 적용되는 숫자로 주로 디지털 장치와 관련된 지식 분야에서 사용됩니다. 그러나 최근에는 16 진법으로 대체되었으므로 사용 빈도가 훨씬 적습니다.

이진 십진법 시스템

이진수로 많은 수의 표현사람에게는 프로세스가 다소 복잡합니다. 이를 단순화하기 위해 2 진 10 진수 시스템이 개발되었습니다. 전자 시계, 계산기에 주로 사용됩니다. 이 시스템에서는 정수가 10 진수 시스템에서 2 진수 시스템으로 변환되지 않지만 각 숫자는 2 진 시스템에서 해당 0과 1 세트로 변환됩니다. 마찬가지로 이진 시스템에서 십진수로 전송됩니다. 4 자리 숫자 0과 1로 표시된 각 숫자는 십진수 시스템의 숫자로 변환됩니다. 원칙적으로 어려운 것은 없습니다.

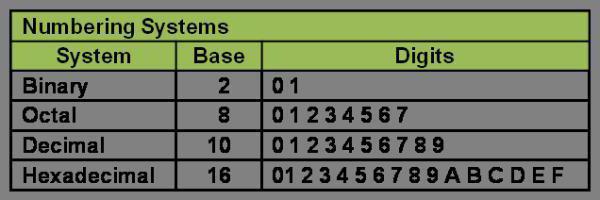
이 경우 숫자를 사용하기 위해 숫자 시스템 테이블이 유용하며 숫자와 이진 코드 간의 통신이 표시됩니다.

16 진법 체계

최근 인기 상승프로그래밍 및 컴퓨터 과학에서 숫자 시스템은 16 진수입니다. 0에서 9까지의 숫자뿐만 아니라 라틴 문자 A, B, C, D, E, F도 사용합니다.

동시에 각각의 문자는 자체 의미를 가지므로 A = 10, B = 11, C = 12 등이됩니다. 각 숫자는 001F라는 4 자로 구성됩니다.

숫자 변환 : 10 진수에서 2 진수로

번호 체계의 번역은 특정 규칙에 따라 발생합니다. 2 진수에서 10 진수로 또는 그 반대로 가장 일반적인 전송입니다.

10 진수의 숫자를 번역하려면시스템을 바이너리로 만들려면 번호 시스템의 밑수, 즉 2로 계속해서 나눠야합니다. 동시에, 각 부서의 나머지는 기록되어야합니다. 이것은 나눗셈의 나머지가 1보다 작거나 같아 질 때까지 발생합니다. 열에서 계산을 수행하는 것이 가장 좋습니다. 그런 다음 나눗셈 결과의 나머지는 역순으로 문자열로 작성됩니다.

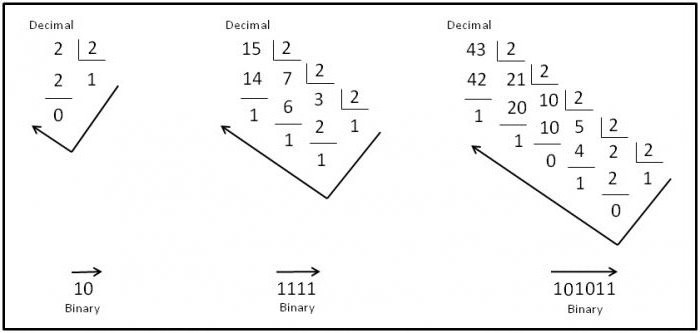
예를 들어 숫자 9를 2 진 시스템으로 변환하십시오.

우리는 숫자가 완전히 나뉘어 있지 않기 때문에 9를 나눈 다음 숫자 8을 취하고 나머지는 9 - 1 = 1이됩니다.

8을 2로 나누면 4가됩니다. 숫자가 완전히 나뉘어져 있기 때문에 다시 나눕니다 - 나머지는 4 - 4 = 0이됩니다.

2와 동일한 연산을 수행합니다. 나머지에서는 0을 얻습니다.

나누기의 결과로 우리는 1을 얻는다.

그런 다음 우리가받은 모든 잔여 물을 역순으로 써서, 총 나누기 1001부터 시작합니다.

총 숫자 체계와 관계없이 십진수에서 다른 숫자로 숫자를 변환하는 것은 위치 시스템을 기준으로 숫자를 나누는 원칙에 따라 결정됩니다.

번역 수 : 바이너리에서 십진수로

바이너리에서 숫자를 10 진수로 변환하는 것은 상당히 쉽습니다. 이를 위해서는 권력을 키우는 규칙을 아는 것만으로 충분합니다. 이 경우에, 2의 힘에.

번역 알고리즘은 다음과 같습니다. 이진수의 코드에서 각 자릿수는 2로 곱해야하며 처음 두 개는 m-1의 제곱이고 두 번째 것은 m-2 등입니다. 여기서 m은 코드의 자릿수입니다. 그런 다음 더하기 결과를 더하여 정수를 얻습니다.

학생들에게는이 알고리즘을보다 간단하게 설명 할 수 있습니다.

우선 우리는 각 자릿수에 2를 곱한 값을 취하고 적어 놓은 다음 0에서 시작하여 끝에서부터 2의 거듭 제곱을 구합니다. 그런 다음 결과 번호를 추가하십시오.

예를 들어 앞에서 구한 1001을 분석하여 십진법으로 옮기고 동시에 계산의 정확성을 검증하십시오.

다음과 같이 보입니다.

1 * 2³ + 0 * 2²+ 0 * 2¹+1 * 2⁰= 8 + 0 + 0 + 1 = 9이다.

이 주제를 공부할 때 2의 제곱을 가진 테이블을 사용하는 것이 편리합니다. 이렇게하면 계산을 수행하는 데 필요한 시간이 크게 줄어 듭니다.

기타 번역 옵션

경우에 따라 양도가2 진수와 8 진수 시스템 사이에서, 2 진수와 16 진수. 이 경우 탭에서 "프로그래머"옵션을 선택하여 특수 테이블을 사용하거나 컴퓨터에서 계산기 응용 프로그램을 실행할 수 있습니다.

산술 연산

어떤 형식이든 관계없이숫자가 표시되면 우리에게 평상시와 같은 계산을 수행 할 수 있습니다. 선택한 숫자 시스템에서 나누기 및 곱하기, 빼기 및 더하기를 할 수 있습니다. 물론 각각의 규칙에는 자체 규칙이 있습니다.

따라서 바이너리 시스템의 경우 각각의 작업에 대해 자체 테이블을 개발했습니다. 동일한 테이블은 다른 위치 시스템에서 사용됩니다.

그 (것)들을 배우는 것은 필요하지 않다 - 다만 인쇄하고 가지고 가십시오. PC에서 계산기를 사용할 수도 있습니다.

컴퓨터 과학에서 가장 중요한 주제 중 하나는 시스템입니다.표기법. 이 주제에 대한 지식, 한 시스템에서 다른 시스템으로 숫자를 전송하기위한 알고리즘에 대한 이해는 알고리즘 및 프로그래밍과 같은보다 복잡한 주제를 이해하고 첫 번째 프로그램을 직접 작성할 수 있음을 보증합니다.